简介
- 对于任意一个无向图,我们必须不重复地走过所有的边(点可以不走完,也可以重复走),求方案是否存在,并输出其中一种(应该是最小字典序。
题目链接:P7771 欧拉路径
结论及推导
我们先来看一下这个两个图
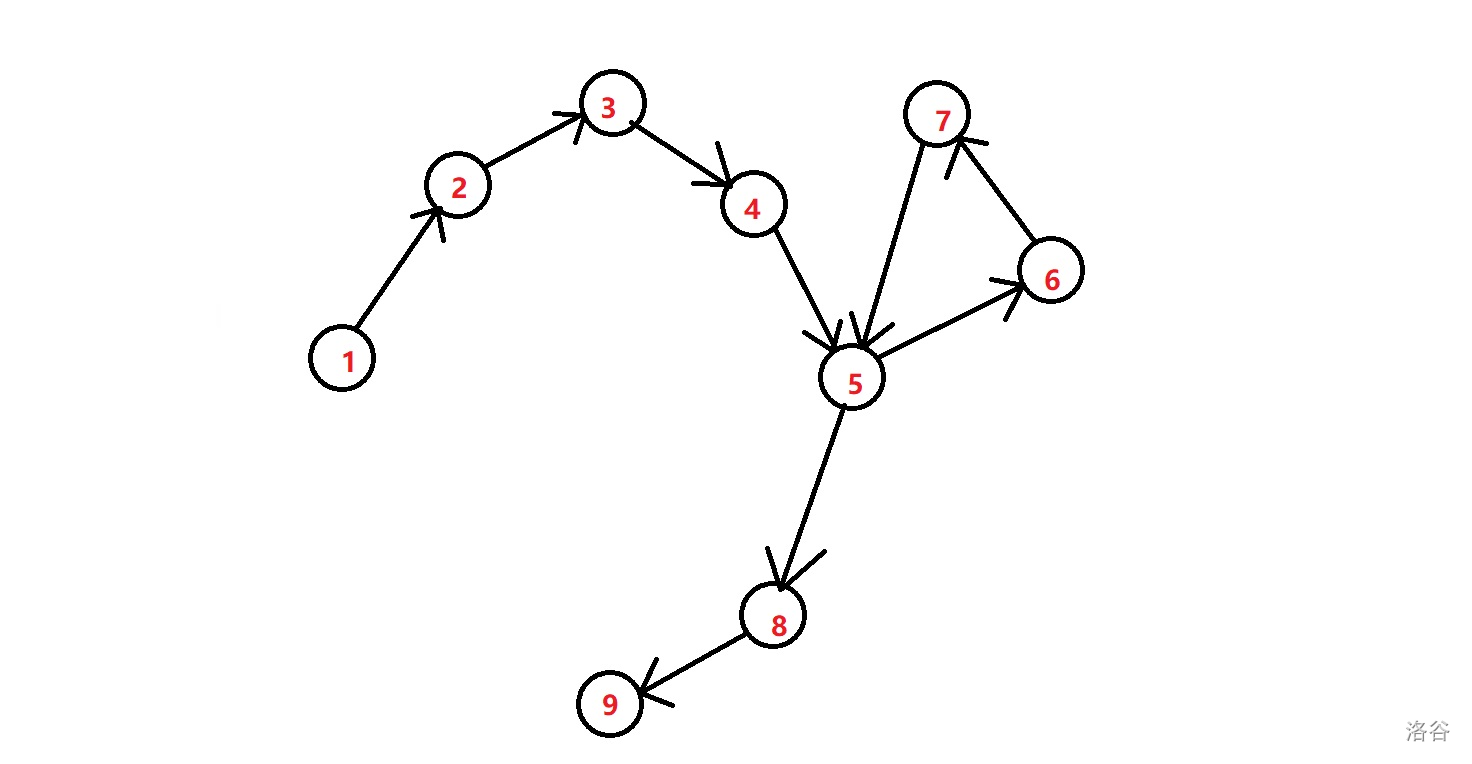
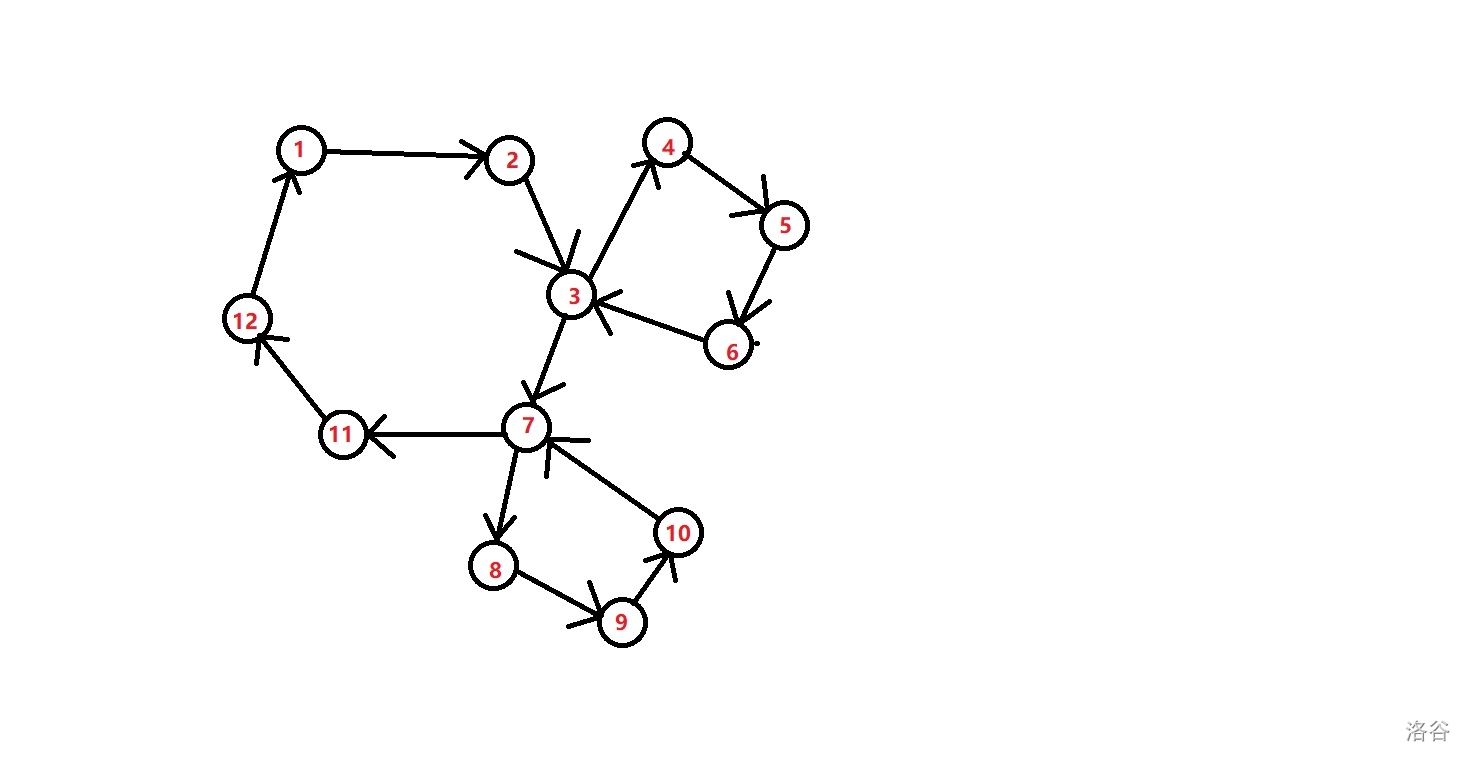
从这两个图中我们不难发现:
1.对于无向图,所有边联通。
(1).存在欧拉路径的充分必要条件:度数为奇数的点只能有0个或两个。
(2).存在欧拉回路的充分必要条件:度数为奇数的点只能有0个
2.对于有向图,所有边都是连通的
- (1).存在欧拉路径的充分必要条件:要么所有点的出度均等于入度;要么除了两个点之外,其余所有点的出度等于入度,剩余的两个点:一个满足出度比入度多1(起点),另一个满足入度比出度多1(终点)
- (2)存在欧拉回路的充分必要条件:所有点的出度均等于入度.
实现
- 我们任意取一个点,然后进行dfs,每次递归到下一层(如果求最小字典序就取最小的)一边递归,一边存储路径,当dfs结束之后,倒序输出(应该不用解释吧)
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
using namespace std;
const int N = 2e5 + 5;
int n, m;
int ru[N], cu[N];
int idx;
vector<int>k[N];
int o[N];
int root, End;
int st[N], l;
void dfs(int x)
{
while(o[x] < k[x].size())
{
int j = k[x][o[x]];
// cout<<"x : " << x << " " << o[x] << " " << k[x].size()<< endl;
cu[x] ++;
ru[j] ++;
o[x] ++;
dfs(j);
}
}
bool vis[N];
void dfs1(int x)
{
while(o[x] < k[x].size())
{
int j = k[x][o[x]];
o[x] ++;
dfs1(j);
}
st[++ l] = x;
}
int main()
{
scanf("%d%d", &n, &m);
for(int i = 1;i <= m;i ++)
{
int p, u;
scanf("%d%d", &p, &u);
k[p].push_back(u);
}
for(int i = 1;i <= n;i ++)
{
sort(k[i].begin(), k[i].end());
}
for(int i = 1;i <= n;i ++)
{
if(o[i] < k[i].size()) {dfs(i); break;}
}
int u = 0;
for(int i = 1;i <= n;i ++)
{
if(cu[i] != ru[i]) u ++;
if(cu[i] == 0 && ru[i] == 0) u = 1;
if(cu[i] == ru[i] + 1) root = i;
if(ru[i] == cu[i] + 1) End = i;
}
if(u != 0 && u != 2)
{
puts("No");
return 0;
}
if(!root && !End) root = End = 1;
memset(o, 0, sizeof(o));
dfs1(root);
for(int i = l;i >= 1;i --)
{
printf("%d ", st[i]);
}
return 0;
}