CF453C Little Pony and Summer Sun Celebration

一道有意思的树形dp

问题

• 给定一个 $n$ 个点， $m$ 条边的无向图和一个01序列，若 $a[i] = 1$ ，则需遍历这个节点奇数次，否则需要遍历此节点偶数次（可以不遍历），求一个可行的方案，要求此方案的长度不超过 $4n$

solution

首先我们观察本题的规律，不难发现：

• 当本图未联通时，任意两个连通块中有需要走奇数遍的点时一定无解（应该不需要解释吧）

• 因为一个节点可能有多个儿子，所以当我们未对当前节点的其他儿子进行判断前，一个可行的策略一定可以是：先处理当前节点的其中一个儿子节点，再从这个儿子节点（儿子节点的子树已经处理完了）回溯到当前节点，接着再由当前节点来处理它的其他儿子并回溯到它的父亲节点（以此递归处理问题）。

• 我们顺着这个思路往下走，将一个需要走奇数次的节点作为根节点，递归处理它的子树，不难发现当我们处理完一个节点的子树，将要回溯到这个节点的父节点时，若这个节点还需要再遍历一遍，我们可以和此节点的父亲节点进行循环（由此节点跳到它的父节点，再由它的父节点跳到它，再由此节点进行回溯，即可更新此节点）。那么根节点如何处理呢？我们进行画图分析：
  

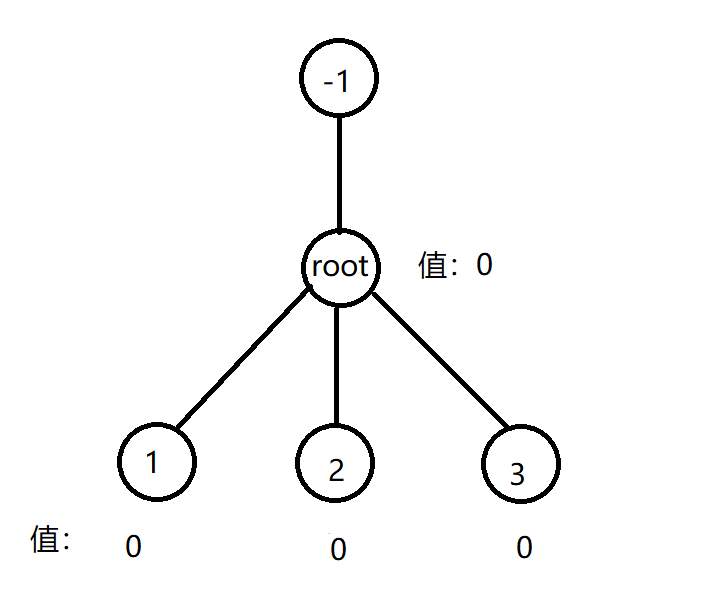
• 此时可以看到3号节点需要回溯了，但根节点不需要被再次遍历，不然根节点会回溯到我们传的-1号虚根节点上，对此，我们只需要进行特判，如果-1号虚根节点入队了，队列数-3（最后3个数应该为 $root$ ，-1 ， $root$ ），即停止从3号节点回溯到根节点，在根节点的前一个节点停止回溯，这样就保证了正确性。

我们再来分析此代码的效率，不难发现每一个叶子节点的最坏入队次数为两次，使其父节点多进队2次，即一个点最多对答案贡献4次，但一定有如同 $root$ 一样的节点，它一定不会和自己的儿子节点循环，所以答案一定严格小于 $4n$ 。

代码

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define LL long long
using namespace std;
const int N = 1e5 + 5, M = N << 1;
int idx;
int e[M], h[N], ne[M];
void add(int x, int y)
{
	idx ++;
	e[idx] = y, ne[idx] = h[x], h[x] = idx;
}
int a[N], root;
bool vis[N];
int st[N << 2], cnt;
void dfs(int x, int father)
{
	vis[x] = 1;
	st[++ cnt] = x;
	a[x] ^= 1;
	for(int i = h[x]; ~i;i = ne[i])
	{
		int j = e[i];
		if(vis[j]) continue;
		dfs(j, x);
		st[++ cnt] = x, a[x] ^= 1;
	}
	if(a[x]) st[++ cnt] = father, st[++ cnt] = x, a[x] ^= 1, a[father] ^= 1;//和父节点循环 
}
int n, m;
int main()
{
	memset(h, -1, sizeof(h));
	scanf("%d%d", &n, &m);
	for(int i = 1;i <= m;i ++)
	{
		int o, u;
		scanf("%d%d", &o, &u);
		add(o, u);
		add(u, o);
	}
	for(int i = 1;i <= n;i ++)
		scanf("%d", &a[i]), root = (a[i] == 1 ? i : root);
	if(!root)//不用遍历就不遍历 
	{
		puts("0");
		return 0;
	}
	dfs(root, -1);
	for(int i = 1;i <= n;i ++)
	{
		if(a[i] == 1)
		{
			puts("-1");
			return 0;
		}
	}
	if(cnt > 1 && st[cnt - 1] == -1) cnt -= 3;//特判 
	printf("%d\n", cnt);
	for(int i = 1;i <= cnt;i ++)
		printf("%d ", st[i]);
    return 0;
}