P1484 种树

为什么每次考试的原题我都没做过呀， $QAQ$

solution

当我们看到这道题时，不难想到这是一道 $dp$ 题。 开个玩笑， $2e5$ 的数据范围，怎么可能 $n ^ 2 Dp$ 。

回到正题：一道经典的带悔贪心。

我们先模拟一下一般的贪心策略，每次选取最大的可取的值，直到不能取为止。

不难发现，这个策略是错的。我们来看一下这个图：

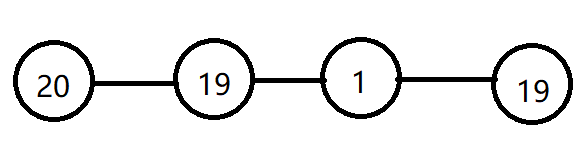
对于第一次策略，我们会优先选择最大的20号点，紧接着，我们就只能憋屈的选择1号点，很明显正解不可能是21， $19+19 = 38$ 明显更优，那么我们应该怎样调整我们的贪心策略才能保证我们贪心的正确性呢，其实并不是很难，我们重新看一幅图。

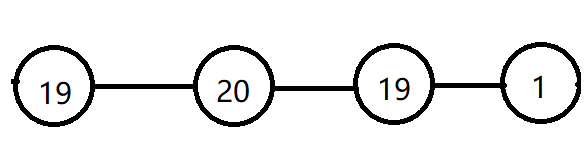
对于这次贪心策略，我们取走20以后顺手删除（左）19点和（右）19点，并将20号点更新为： $19 + 19 - 20 = 18$ ，即：

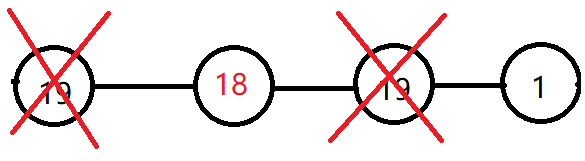
此时，我们再取走18号点，并删除与18号点相邻的1号点，并将 $-17$ 号点加入队列中：

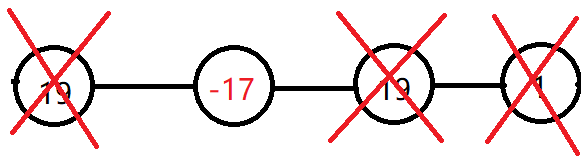
根据题目的意思，现在我们无论取多少都无所谓，所以放弃-17，得到答案38正解，这样不但避免了选择相邻的两个（选一个的时候，另外两个被删除了），还保证了价值守恒（请自行理解），那么这道题就完结撒花啦。

三倍经验：luogu P1792 [国家集训队]种树， luogu P3620 [APIO/CTSC 2007] 数据备份(此题具有一定的思考难度 (主要还是板子))

代码

#include<bits/stdc++.h>
#define LL long long
using namespace std;
const int N = 5e5 + 5;
struct node{
	int l, r;//上一个和下一个的下标  
	LL val;
}a[N];
struct Node{
	int id;
	LL val;
	bool operator <(Node b)const
	{
		return val < b.val;
	}
};
int n, m;
LL ans;
bool vis[N];//判断当前节点是否可选
priority_queue<Node>q;//大根堆维护最大值 
void Del(int x)
{
	a[x].l = a[a[x].l].l;//左右边界移动，删除 x的左右节点 
	a[x].r = a[a[x].r].r;
	a[a[x].l].r = x;
	a[a[x].r].l = x;
} 
int main()
{
	scanf("%d%d", &n, &m);
	for(int i = 1;i <= n;i ++)
	{
		scanf("%lld", &a[i].val);
		a[i].l = i - 1;
		a[i].r = i + 1;
		q.push((Node){i, a[i].val});
	}
	for(int i = 1;i <= m;i ++)
	{
		while(vis[q.top().id]) //延迟删除标记 
			q.pop();
		Node now = q.top();
		q.pop();
		if(now.val < 0) break; 
		ans += now.val;
		vis[a[now.id].l] = vis[a[now.id].r] = 1;
		a[now.id].val = a[a[now.id].l].val + a[a[now.id].r].val - a[now.id].val; 
		q.push((Node){now.id, a[now.id].val});//加入新点 
		Del(now.id);
	}
	printf("%lld", ans);
	return 0;
}