模拟退火

很久之前学的了，这次算是补个漏

简介

• 退火，来自于物理，模拟退火算法来源于固体退火原理，是一种基于概率的算法，将固体加温至充分高，再让其徐徐冷却，加温时，固体内部粒子随温升变为无序状，内能增大，而徐徐冷却时粒子渐趋有序，在每个温度都达到平衡态，最后在常温时达到基态，内能减为最小。

• 模拟退火（下文简称退火）是一种高效的骗分算法，以简单易背的模板和优秀的效率闻名于世（就比暴力好一点），常常用于求解答案是连续不断（接近也行）的函数的最大值或最小值，强于三分，可求解多峰函数。

• 其运行效果如图所示：

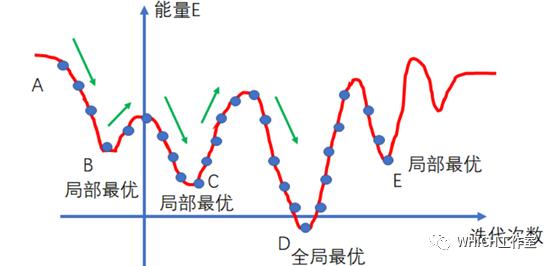
正确性

• 说到随机算法，就一定要考虑其的正确性，退火算法理论上是一种贪心算法，它会尽可能找到离自己更近，且更接近正解的答案的点，然后跳过去。但不同于贪心算法的是，它有一定概率越过这个点，去其他峰试试运气，但越到后期越不容易跳过去，就越趋近稳定。所以，可以肯定的是，它不会只停留在一个峰上，而是会四处寻找其他答案。
• 我们设每一次错误的概率为$0.9999$，但是当我们在这次退火的基础上再加上$50000$次退火，正确性就为：$0.9999^{50001} = 0.0067$ 就是一个极小的概率了，所以退火是一个稳定的正确的算法。

具体实现

• 当我们理解到这个算法是随机的算法时，一定要充分运用到随机的艺术，对于初始温度和结束温度，还有温度变化率一定要在平日里积累经验，这里给出核心代码：

if(exp(-delte / t) < (double)rand() / RAND_MAX)//delte为上一个解和当前解的差值

例题

• 这里以luogu P2503 [HAOI2006]均分数据 为例来简单介绍退火的运用

• 根据题目，不难发现这是DP，但当我们在考场上不会的时候该怎么办呢？根据题目，我们可以发现，当我们更改一个值后，答案并不会增大很多，所以我们可以通过模拟退火解决此题

• 代码：

• #include<iostream>
  #include<cstring>
  #include<cstdio>
  #include<cstdlib>
  #include<cmath>
  #include<algorithm>
  #include<ctime>
  #define x first
  #define y second
  #define PII pair<int, int>
  using namespace std;
  const int N = 25, M = 10, Inf = 0x3f3f3f3f3f;
  int n;
  int w[N], q[N], s[M];
  double ans = 1e8;
  int m;
  int calc()//求解单次答案
  {
      memset(s, 0, sizeof(s));
      for(int i = 0;i < n;i ++)
      {
          int k = 0;
          for(int j = 0;j < m;j ++)
          {
              if(s[j] < s[k]) k = j;
          }
          s[k] += w[i];
      }
      double avg = 0;
      for(int i = 0;i < m; i ++) avg += (double)s[i] / m;
      double res = 0;
      for(int i = 0;i < m;i ++) res += (s[i] - avg) * (s[i] - avg);
      res = sqrt(res / m);
      ans = min(ans, res);
      return res;
  }
  void sim()//退火
  {
      random_shuffle(w, w + n);
      for(double t = 1e4;t > 1e-6;t *= 0.99)
      {
          int a = rand() % n, b = rand() % n;//随机我们交换的数
          double x = calc();
          swap(w[a], w[b]);
          double y = calc();
          double delta = y - x;
          if(exp(- delta / t) < (double)rand() / RAND_MAX) swap(w[a], w[b]);
      }
  }
  int main()
  {
      scanf("%d%d", &n, &m);
      for(int i = 0;i < n;i ++) scanf("%d", &w[i]);
      while((double)clock() / CLOCKS_PER_SEC < 0.8) sim();//决定退火次数
      printf("%.2lf", ans);
      return 0;
  }